Funktion des Pulses
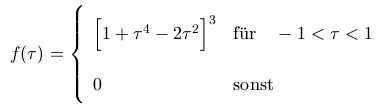
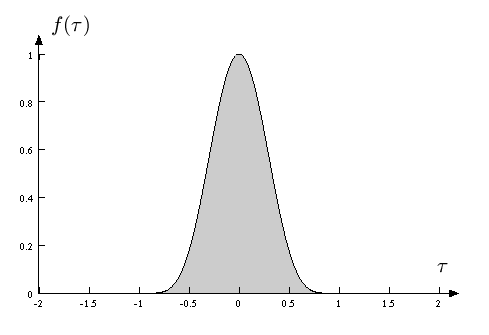
Form des Pulses
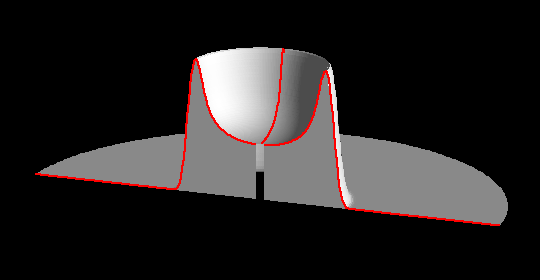
Ausbreitung bei
Rotationssymmetrie
Animation (168kB)
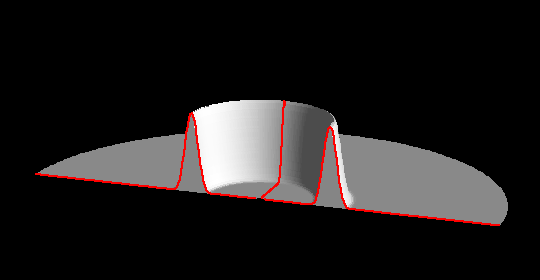
Ausbreitung bei
Kugelsymmetrie
Animation (91kB)
| Gleichung (1)
Funktion des Pulses |
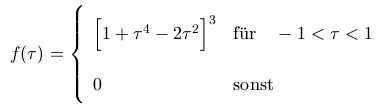 |
| Abbildung (1)
Form des Pulses |
 |
| Abbildung (2)
Ausbreitung bei Rotationssymmetrie Animation (168kB) |
 |
| Abbildung (3)
Ausbreitung bei Kugelsymmetrie Animation (91kB) |
 |