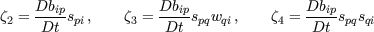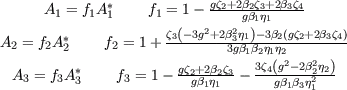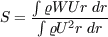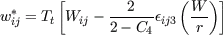|
Streamline curvature has two main impacts on turbulence modelling, one effects the turbulent production and the other is due to convective transport. Only the latter will be discussed here. In the classical approach of the explicit algebraic stress model (EASM) strategy a RSTM is transformed into a set of explicit algebraic expressions using the structural equlibrium assumption
In fact it is only valid if bij and Uk are formulated in a streamline-system (s). A better assumption is consequently given by
where the first term vanishes whereas the last term can be kept as an explicit curvature correction. Models that consider a reduction to the streamline-system and uses this equation have several severe disadvantages: As a result it can be stated that the quality of EASM results depend on the underlying co-ordinate system. Basic tests can be performed for a given velocity field where the transformation can be handled analytically. The structural equilibrium is transformed to an arbitrary calculation co-ordinate system (r):
The resulting tensor
The modified model finally writes
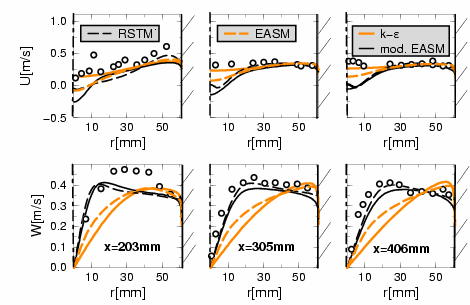
A more general approach to the problem of capturing system rotation and curvature effects can be derived by neglecting the structural equilibrium assumption and keep the substantial derivative on the right hand side of the ASM
with the coefficients Strictly speaking this is not an algebraic model. However, if the substantial derivative is treated explicitly in an implicit framework it can be transformed into a modified EASM. A closure for 2D flows and three independent generators can be found by the projection method of Rung [1]. The method is used to project the extended model into the same two-dimensional three generator functional basis.
with Projection means that bij in the ASM is replaced by this ansatz and is scalar multiplied by each of the base tensors. The resulting system of equation can be used to calculate the EASM coefficients A(l):
with the invariants The linear system of equations can be solved by a symbolic manipulation software and gives the standard model of Gatski and Speziale [4] if all components of the substantial derivative are set to zero. Without the assumption of structural equilibrium, the solution depends on the components of the substantial derivative of the anisotropy tensor. Considering a trace-free bij, only three parameters
This new model is extended by the functions f1, f2 and f3 that appear in the coefficients A(1), A(2) and A(3). The modifications immediately vanish if the substantial derivitative of bij disappears and structural equilibrium is fullfilled. Consequently the model reduces to the standard approach in a streamline based system. In the numerical implementation, the derivitatives of bij have to be handled explicitly, for example based on quantities of the last iteration cycle.
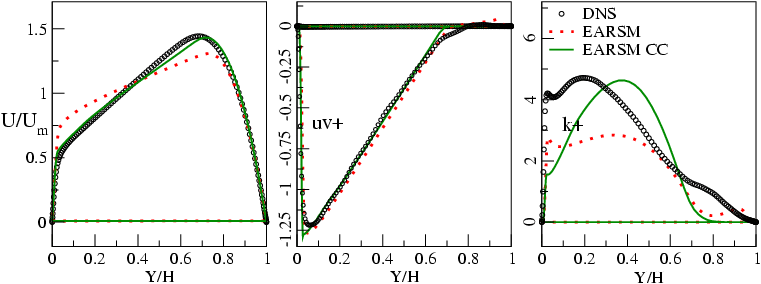
The new approach is applied to a fully developed rotating channel flow [6] that was investigated by Alvelius and Johansson, who performed a DNS for several Reynolds numbers and rotation rates. In the present case, the Reynolds number based on the bulk velocity Um and the channel width h is fixed at Rem=6892. The case with the strongest rotation and a Rosby number of Ro=0.77 is considered. Numerial results of the proposed method are compared to the DNS data and other current alternative curvature correction methods. Four different modelling practices are performed: All models use the FRLT set of coefficients [1]:
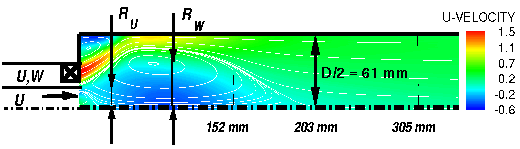
The production-to-dissipation ratio, appearing in the g coefficient is handled in the self-consistent technique of Wallin & Johansson [7] in all models. Due to the strong rotation, the turbulent flow is stabilized near one of the channel walls whereas it is unstable near the opposite wall. Consequently, the Reynolds number based on the friction velocity increases at the unstable channel wall, which is predicted by all models and the DNS. However, the Reynolds number predicted by the approaches considered differ significantly. This is due to the predicted profiles and levels of stresses in the upper und lower channel boundary layer. Results are plotted in figure 1. The standard EASM based on the structural equilibrium assumption underpredicts the effect of system rotation and gives the least steep velocity profile. It can be improved by the curvature correction method. The new non-equilibrium-based approach is able to give satisfying predictions of both velocity and shear-stress. In the present rotating channel case, the model equation could be solved until complete convergence where the solution is supposed to be identical to the underlying RSTM. It has to be noted that in the implementation of the non-equilibrium approach, the functions f1, f2 and f3 as well as the substantial derivatives itself must be limited. The limitation has a strong influence on the convergenece behaviour of the whole procedure even for the very simple case of the rotating channel flow.
Figure 1: Mean velocity, turbulent shear stress and turbulent kinetic energy in the rotating channel flow at Re = 6892 and Ro = 0.77. Numerical results compared to DNS data by Alvelius and Johansson [6]. First application of the streamline curvature correction is a swirling flow in a combustion chamber which has been investigated experimentally by Johnson & Roback [3]. The important flow properties are summarised in table 1 with the Reynoldsnumber based on a bulk velocity, the radius and the swirling number S
Flow simulations are performed on a 120x80 cell mesh covering about 100 diameters in mean flow direction. A zero-gradient condition is used at the outlet whereas the inflow values are taken from a simulation of the pipe flow upstream. In this flow strong streamline curvature occurs due to the strong swirl. The streamlines can be assumed as cylindrical with a constant azimuthal velocity W. In this case the transformation simplifies resulting in
Figure 2: Strongly swirling flow in a combustion chamber by Johnson & Roback [3] (Re=47500, S=0.45). Due to the described deficiencies of linear eddy-viscosity
approaches these models are not able to mimic the effect of vortex-breakdown.
Isotropic models usually predict a linear rise of the azimuthal velocity
similar to a solid-body motion. In figure 3 the
An EASM extended by the curvature correction
based on an assumed The present investigations show that curvature correction has a great potential for both linear eddy-viscosity and explicit algebraic stress models with respect to swirling flows and similar technical applications. |
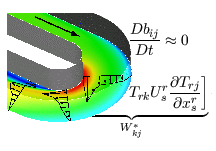
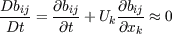 with
with
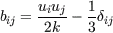
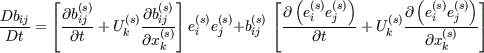
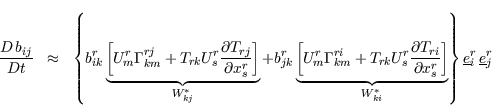
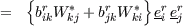
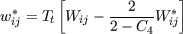
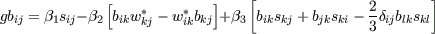
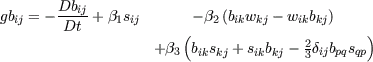
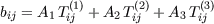
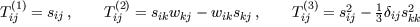
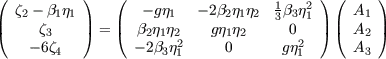
 .
.