|
|
|
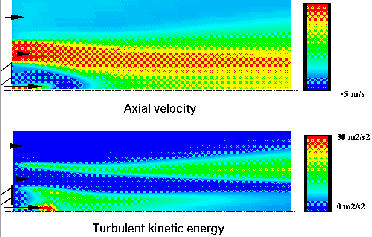
| Fig. 3: Bluff-body burner; axial velocity and turbulence energy |
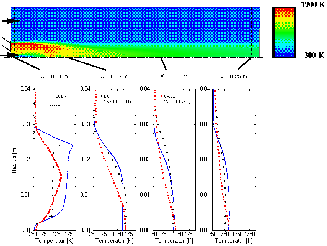
Fig. 4: Bluff-body burner; radial temperature profiles |

|

|
|
| Fig. 3: Bluff-body burner; axial velocity and turbulence energy |
Fig. 4: Bluff-body burner; radial temperature profiles |
A review of recent attempts to simulate periodic turbulent flows displays a considerable disparity in their predictive capabilities. Generally, an accurate computational representation of of complex transient flows is exclusively within reach of direct numerical simulation (DNS) or large-eddy simulation (LES). Due to the extrem computational demands, the application of these structure resolving methodologies is confined to flows at low & moderate Reynolds numbers in simple geometries. Thus, simulations based on Reynolds- or phase-averaged Navier-Stokes equations in conjunction with an empirical turbulence closure model are a viable route to approach these flows for their robustnesss, geometrical flexibility and computational efficiency.
|
|
|
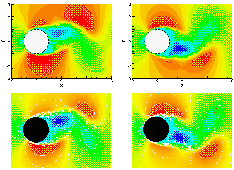
| Fig. 5: Circular cylinder at Re=500; phase-averaged streamlines (phase 01 and 09) from DNS and RANS |
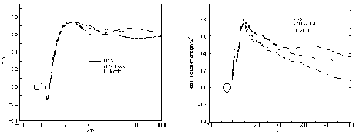
Fig. 6: Mean velocity and total energy distribution on the centre plane of the circular cylinder |
The principal aim of the study is to analyze a class of recently developed efficient turbulence closure models with respect to the accuracy of flow physics representation in periodic turbulent flows. Therefore Non-linear eddy-viscosity models and explicit algebraic stress models up to cubic fragments of strain-rate and vorticity tensors are in the focal point, however the preformance of a selected realizable linear truncation is also given for completness.

|
1 2 3 4 5 6 |

|