Superficially, the failure of the standard Boussinesq-viscosity model could -at least to some extent- be traced back to their inability to mimic the distinct influence of rotational and irrotational distortion of the flow. Non-linear eddy-viscosity models or explicit algebraic stress models are a viable approach to remedy the shortcomings of the linear eddy-viscosity model, while retaining important numerical advantages of the concept. They are often seen to offer accurate predictive response to streamwise curvature and non-inertial effects. A typical feature of all these attempts is that they lean on constitutive relations linking the Reynolds stresses to non-linear expressions of strain rate and vorticity components which effectively gives rise to an anisotropic eddy-viscosity coefficient.

Phase-averaged streamlines (phase 01)
Fig.12: Vortex Shedding behind a Square Cylinder at Re=22 000, Phase-averaged streamlines (phase 01)

  Contribution Cd,time Cd,phase Cd,rms Cl,phase Cl,rms St  lr
      Experiment   (Lyn et al., 1995)2 2.1 - - - - 0.132 1.38
      LES               (Breuer et al., 1995)3 2.3 - 0.14 - 1.15 0.130 1.46
  Linear EVM
      LLR k-w             (Rung & Thiele, 1996) 1 2.268 2.428 0.095 2.04 1.380 0.149 1.09
      Two-layer k-e   (Bosch & Rodi, 1995)9 1.72 -   0. - 0.426 0.137 1.25
  Non-linear EVM
      EASM    (Fu, Rung & Thiele, 1998; quadratic version)4 2.24 2.424 0.072 1.90 1.368 0.144 1.230
      NLEVM (Craft, Launder & Suga, 1996; cubic version)7 2.27 2.405 0.107 2.12 1.534 0.135 1.225
      NLEVM (Lien, Chen & Leschziner, 1996) 5 2.18 2.490 0.187 2.08 1.538 0.128 1.223
      NLEVM (Gatski & Speziale,1993; quadratic version)6                             NO RESULTS   (Calculation aborted) ! 
  RSTM
       RSTM two-layer  (Franke & Rodi, 1993)8 2.43 2.079 0.06 1.84 1.300 0.159 1.00
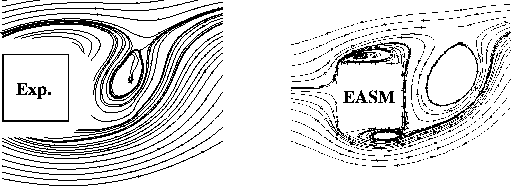
Tab.2: Vortex Shedding behind a Square Cylinder at Re=22 000, Global Flow Parameters

[1]  T. Rung  et al.:  9th. Int. Symp. of Transport Phenomena in Thermal-Fluids Eng., pp. 321,Singapore, 1996.
[2]  D. Lyn et al.:  J. Fluid Mech., 304, pp. 285., 1993.
[3] W. Rodi et al.:  ASME J. Fluids. Eng., 119, pp. 248, 1997.
[4] T. Rung et al.: 4th Int. Symp. on Eng. Turbulence Modelling and Measurements, Corsica, 1999.
[5] F.S. Lien et al.: 3rd. Int. Symp. on Eng. Turbulence Modelling and Measurement, pp. 91, Crete, 1996.
[6] T.B. Gatski et. al.:   J. Fluid Mech., 254, pp. 59, 1993.
[7] T.J. Craft et al.: Int. J. of Heat and Fluid Flow, 17, pp. 108, 1996.
[8] R. Franke et al.: 9th. Symp. on Turblent Shear Flows, Kyoto, 1993.
[9] G. Bosch et al.: 10th Symp. on Turblent Shear Flows, Pennsylvania State Univ., 1995.
[10] K. Abe et al.: Int. J. Heat Mass Transfer, 37, pp. 139, 1994.
[11] H. Persillion: Internal Rport HFI-TU Berlin, 1997.
 

1 2 3 4 5 6

Webmaster
Last modified: Mon Apr 26 14:30:49 CEST 1999