


Next: Wing-Body Configuration at High
Up: High-Lift Flows
Previous: High-Lift Flows
Figure 9:
Three-element aerofoil: pressure coefficient and streamlines at maximum lift, SALSA computation
|
|
A three-element aerofoil in landing
configuration, Fig. 9, is computed at 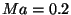 ,
,
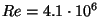 and various
angles-of-attack including cases beyond maximum lift. The goal of these
simulations is to determine the various turbulence models' capability to
predict maximum lift and - at least qualitatively - the lift characteristics
beyond stall. A grid with 75,177 points and 9 blocks supplied by DLR is used. A
and various
angles-of-attack including cases beyond maximum lift. The goal of these
simulations is to determine the various turbulence models' capability to
predict maximum lift and - at least qualitatively - the lift characteristics
beyond stall. A grid with 75,177 points and 9 blocks supplied by DLR is used. A
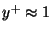 is aspired, however, this could not be guaranteed over all parts of the
configuration, so that locally a
is aspired, however, this could not be guaranteed over all parts of the
configuration, so that locally a
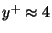 has to be tolerated. The
FLOWer code is employed for the computations, the models investigated include
LLR
has to be tolerated. The
FLOWer code is employed for the computations, the models investigated include
LLR 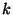 -
-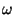 (albeit with a slightly modified
(albeit with a slightly modified 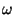 -equation), LEA
-equation), LEA
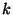 -
-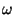 , SALSA and Spalart-Allmaras. As the transition locations are not
known, the computations are performed in a fully turbulent fashion.
Furthermore, a steady time-marching technique is used since unsteady
computations turned out to be prohibitively expensive. This does not constitute a proper validation
approach, however, it reflects current industrial methodology.
, SALSA and Spalart-Allmaras. As the transition locations are not
known, the computations are performed in a fully turbulent fashion.
Furthermore, a steady time-marching technique is used since unsteady
computations turned out to be prohibitively expensive. This does not constitute a proper validation
approach, however, it reflects current industrial methodology.
Fig. 10 displays the computed and measured lift coefficients versus the
angle-of-attack, where noticeable differences are visible between the different
models evaluated. Wilcox 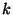 -
-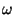 is not included in this comparison, as the
results are very similar to the LEA
is not included in this comparison, as the
results are very similar to the LEA 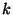 -
-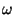 ones. The lift coefficients are
averaged over a certain amount of multigrid cycles after convergence was
reached save some oscillations, which, however, hint to flow unsteadiness.
ones. The lift coefficients are
averaged over a certain amount of multigrid cycles after convergence was
reached save some oscillations, which, however, hint to flow unsteadiness.
Figure 10:
Three-element aerofoil: lift coefficient vs. angle-of-attack for various turbulence models
|
|
In the region well below maximum lift, all models except SALSA slightly
overpredict the lift coefficient, whereas SALSA shows a severe underprediction.
In this regime, the flow is separated over the rear part of the flap, which is
basically resolved by all models. However, the separation length determined by
SALSA is obviously too large, which in turn reduces the suction peak not only
on the flap but also the slat and the main wing. Approaching maximum lift, the
flow over the flap reattaches. Up to maximum lift, the flow remains attached
over the whole geometry, see Fig. 9, leading to very similar results for all
models investigated, except for LLR 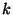 -
-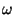 , which yields a lift coefficient
too low due to an off-surface recirculation zone above the flap affecting the
circulation over the whole configuration. If the angle-of-attack is increased
beyond this point, LLR
, which yields a lift coefficient
too low due to an off-surface recirculation zone above the flap affecting the
circulation over the whole configuration. If the angle-of-attack is increased
beyond this point, LLR 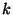 -
-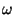 and SALSA show a severe breakdown in lift,
which is not found by LEA
and SALSA show a severe breakdown in lift,
which is not found by LEA 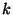 -
-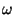 and Spalart-Allmaras. The reason for
this, however, is different for both models. For SALSA, in the stalled regime,
despite the flow over the flap being fully attached, separation occurs on the
upper slat surface significantly reducing the suction peak on the slat as well
as the overall pressure level on the main aerofoil. According to [20], the
latter is caused by a larger slat wake deficit in the slat-separated case
leading to a loss of near-surface momentum on the main profile. As can be seen
in Figs. 11 and 12, where the pressure coefficient distributions are given
for three different angles-of-attack as determined using the one-equation
models, this flow feature is captured by SALSA, whereas Spalart-Allmaras misses
it completely, mistakenly leading to very similar predictions for the maximum lift and the
stall case. Furthermore, an off-surface flow reversal region situated in the
wake of the flap is observed in the SALSA computations, which is not present in
the Spalart-Allmaras results. LLR
and Spalart-Allmaras. The reason for
this, however, is different for both models. For SALSA, in the stalled regime,
despite the flow over the flap being fully attached, separation occurs on the
upper slat surface significantly reducing the suction peak on the slat as well
as the overall pressure level on the main aerofoil. According to [20], the
latter is caused by a larger slat wake deficit in the slat-separated case
leading to a loss of near-surface momentum on the main profile. As can be seen
in Figs. 11 and 12, where the pressure coefficient distributions are given
for three different angles-of-attack as determined using the one-equation
models, this flow feature is captured by SALSA, whereas Spalart-Allmaras misses
it completely, mistakenly leading to very similar predictions for the maximum lift and the
stall case. Furthermore, an off-surface flow reversal region situated in the
wake of the flap is observed in the SALSA computations, which is not present in
the Spalart-Allmaras results. LLR 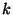 -
-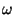 , on the other hand, shows a large
recirculation region affecting not only the flap but also the main aerofoil.
Thus, the flow topology in the stalled case is different for LLR
, on the other hand, shows a large
recirculation region affecting not only the flap but also the main aerofoil.
Thus, the flow topology in the stalled case is different for LLR 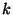 -
-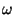 and
SALSA, with the prediction of the latter probably being more realistic.
and
SALSA, with the prediction of the latter probably being more realistic.
As it is unclear to date which physical mechanisms constitute the lift-limiting
mechanism [20], and also taking the aforementioned limitations into
account, final conclusions concerning the models' capabilities cannot be drawn
here. However, the ability of LLR 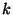 -
-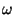 and SALSA to generally predict
stall at about the correct angle-of-attack is a promising feature for future
investigations on such configurations. LEA
and SALSA to generally predict
stall at about the correct angle-of-attack is a promising feature for future
investigations on such configurations. LEA 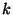 -
-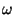 in turn, which has shown
promising results in transonic flows, behaves like the standard approaches
here, which, in all likelihood, can be attributed to the fact that LEA is cast
in terms of the original Wilcox background model.
in turn, which has shown
promising results in transonic flows, behaves like the standard approaches
here, which, in all likelihood, can be attributed to the fact that LEA is cast
in terms of the original Wilcox background model.
Figure 11:
Three-element aerofoil: pressure coefficient distribution for the Spalart-Allmaras model
|
|
Figure 12:
Three-element aerofoil: pressure coefficient distribution for the SALSA model
|
|



Next: Wing-Body Configuration at High
Up: High-Lift Flows
Previous: High-Lift Flows
Martin Franke
2003-10-22
![\includegraphics[width=90mm]{2dhl_camax.eps}](img28.png)
![\includegraphics[width=90mm]{2dhl_camax.eps}](img28.png)
![]() -
-![]() is not included in this comparison, as the
results are very similar to the LEA
is not included in this comparison, as the
results are very similar to the LEA ![]() -
-![]() ones. The lift coefficients are
averaged over a certain amount of multigrid cycles after convergence was
reached save some oscillations, which, however, hint to flow unsteadiness.
ones. The lift coefficients are
averaged over a certain amount of multigrid cycles after convergence was
reached save some oscillations, which, however, hint to flow unsteadiness.
![\includegraphics[width=120mm]{2dhl_cl.eps}](img32.png)
![]() -
-![]() and SALSA to generally predict
stall at about the correct angle-of-attack is a promising feature for future
investigations on such configurations. LEA
and SALSA to generally predict
stall at about the correct angle-of-attack is a promising feature for future
investigations on such configurations. LEA ![]() -
-![]() in turn, which has shown
promising results in transonic flows, behaves like the standard approaches
here, which, in all likelihood, can be attributed to the fact that LEA is cast
in terms of the original Wilcox background model.
in turn, which has shown
promising results in transonic flows, behaves like the standard approaches
here, which, in all likelihood, can be attributed to the fact that LEA is cast
in terms of the original Wilcox background model.